Similar triangles have a similar shape, but are not necessarily equal in size. If triangles are similar their length of sides is proportional and the corresponding angles are equal. The ratio between these sides is termed the scale factor. We often use small tick marks to demonstrate angles that are equal in diagrams of similar figures. This topic goes hand-in-hand with ratios and proportions. We would suggest a brief review before starting this section. These worksheets offer an opportunity to practice working with similar triangles. Your students will use these activity sheets in order to practice using proofs to determine segment lengths, calculate ratios, and more, of similar triangles.
Print Identify Similar Triangles Worksheets
Click the buttons to print each worksheet and associated answer key.
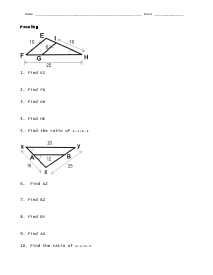
Triangle Proofs Worksheet
Students will find the lengths of sides of triangles by using the indicated data. There are two triangle diagrams and five problems are provided for each.
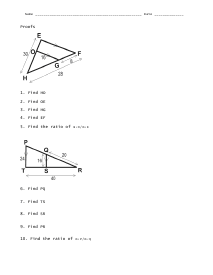
Proofs Practice
Students will find the measures of the segments as indicated. Two diagrams and ten problems are provided.
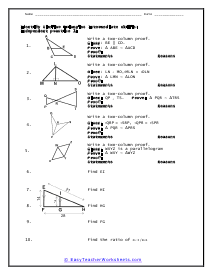
Similar Triangles Proofs Intermediate Skills
Students will write a two-column proofs on this worksheet. Use all of the given information to make sense of all of these shapes. Ten problems are provided.
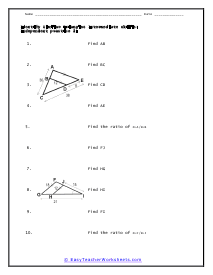
Similar Triangles Identification
Based on the measures of two triangles students will find all types of different measures. Two diagrams and ten problems are provided.
Similar Triangles Knowledge Check
Two diagrams are given. Students will use them to find the measures of the indicated segments. This is a good worksheet to help you understand how well you know this topic.
How Do You Identify Similar Triangles?
Similar figures share the same shape. We can identify this through a number of means. If we have all their measures, that's simple! Many times we do not know all the measures or are at least missing a few of them. Most commonly we will look for corresponding angles and sides.
We can easily identify similar triangles by applying three similarity theorems specific to triangles. These three ways to prove the similarity of triangles involve, side-angle -side (SAS), Angle- Angle (AA), and Side-Side-Side (SSS). These three methods are used to establish the congruence of the triangles. We employ these theorems to know that congruence of the corresponding angles and the sides are proportional. One advantage of employing these theorems is that we do not have to know all six measurements of the triangle.
Side-Angle-Side (SAS) Theorem - This theorem follows the order of a side, an included angle, and then a side. The SAS theorem says that two triangles are similar if two sides of a triangle are proportional to the two corresponding sides of second triangles, and the included angles are congruent.
Side-Side-Side (SSS) Theorem - The last theorem telling us about the congruency of a triangle, states that if all three sides of one triangle are proportional to all three corresponding sides of the second triangle, then those two triangles are congruent.
Angle-Angle (AA) Theorem - Angle-Angle (AA) theorem says that two triangles are similar if the two pairs of their corresponding angles are congruent. These two triangles might appear as identical. To establish two triangles as congruent using this theorem, you only have to compare the two pairs of corresponding angles.


